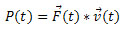Teljesítménymérés II.

Fékgéppel nem rendelkező padon, instacioner motorüzemben végzett és a fékgéppel szerelt görgős padon meghatározott gyorsulási karakterisztika mentén történő teljes terheléses mérés kivitelezése egymással megegyezik. Röviden: a görgős pad kerékágyába beállnak a jármű hajtott kerekeivel, a járművet (általában) spaniferrel rögzítik. A rögzítéssel nem csak a jármű előre-hátra történő esetleges elmozdulását minimalizálják, hanem az oldalirányba való kóválygást is meggátolják. Ezután a görgő kerületi sebessége és a motor fordulatszáma közti áttételt felveszik. A motor fordulatszámának megállapítása különféle módszerrel történhet, a mai korszerű autóknál már lehetőség van arra, hogy a mérőpad számítógépe a motorfordulat aktuális értékét a jármű OBD csatlakozóján keresztül közvetlenül kapja. Ezután alacsony fordulatszámról direkt fokozatban (direkt áttételhez legközelebbi fokozatban, a hajtáslánc mechanikai veszteségének minimalizálása érdekében) teljes gázzal fordulatszámtiltás-közelig, vagy az előre meghatározott legnagyobb mérési fordulatszámig pörgetik a motort,  a fordulatszámtiltás közelében a tengelykapcsoló segítségével oldják a hajtásláncot és mérik a hajtáslánc szöglassulását a kerekek (közel) megállásáig. A kétféle pad (és mérési módszer) közti különbség: az instacioner pad esetén a görgők tehetetlenségi nyomatéka (a gyorsulás ellen dolgozó tényező) állandó, míg fékgépes padnál a gyorsulás ellen ható fékezőerő (nem a pad tehetetlenségi nyomatéka!) szabályozható.  Azaz, ha nagy tehetetlenségi nyomatékú forgórendszerrel rendelkező padon mérünk egy relatíve kis teljesítményű autót, akkor a motor lassan fog felpörögni, mert nehezen birkózik meg a görgők gyorsításával. Azonban ha ugyanezen a padon egy nagyon nagy teljesítményű autót mérünk, akkor a motorfordulat tiltásig való felfutása igen rövid idő alatt mehet végbe, ami a mérés kivitelezését megnehezíti, a fordulatszámtiltáskor fellépő vibráció a jármű görgőágyban való stabilitását veszélyezteti, a kerékszlip észlelése a nagyon gyors felpörgés miatt nehéz.  Régebbi, lassú mintavételezéssel dolgozó padnál akár mérési problémát is jelenthet a görgők nagyon gyors felpörgetése. A fékgépes pad előnye itt is megmutatkozik: a vizsgált jármű teljesítményéhez állítható a görgő forgatásához szükséges erő, így a teljes fordulatszám-tartományban a járművet előre rögzített gyorsulási karakterisztika mentén lehet vizsgálni. Két videó a mérés végrehajtásáról:

Az operátor szemszögéből (a hengerenkénti pillangószelepesre (ITB) átépített Clio RS gyönyörű, jellegzetes szívóhangja jól hallható):

Méréskor a sebesség függvényében a teljes terheléses gyorsítás szakaszában meghatározásra kerül a kerékteljesítmény értéke, majd szabadkifutásos szakaszban a hajtáslánc  fékezőteljesítménye (a motor lendkereke és a görgős pad közötti "rész" veszteségteljesítménye). A hajtáslánc-veszteség számítással csak becsülhető, pontosan nem meghatározható, ezért szükséges ennek  mérése.  A diagnosztikai célú teljesítményméréshez minimálisan 5%-os, elvárhatóan 3%-os pontosság szükséges.

A továbbiakban fékgép nélküli padon történő instacioner motorüzemben végzett vizsgálat kerül tárgyalásra.

Teljes terheléses gyorsítás

A teljes gázzal történő gyorsítás során a motor-hajtáslánc-fékpad egy közös forgórendszert alkot:

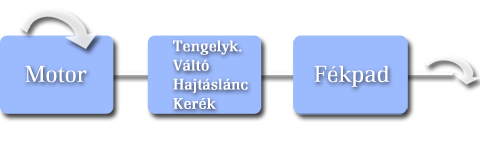
A korábban említett fizikai összefüggések alapján ekkor:

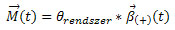ahol:
M: a rendszert gyorsító nyomaték [Nm]
thetarendszer= thetamotor + thetahajtáslánc + thetapad [kgm^2] a teljes rendszer tehetetlenségi nyomatéka a görgős pad tengelyére redukálva
béta: kerék (pozitív) szöggyorsulása [1/s^2]

A gyorsításhoz szükséges teljesítmény:

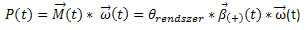ahol:
thetarendszer= thetamotor + thetahajtáslánc + thetapad [kgm^2] a teljes rendszer tehetetlenségi nyomatéka a görgős pad tengelyére redukálva
béta: rendszer szöggyorsulása [1/s^2] (a pozitív index a gyorsulásra utal)
omega: a rendszer szögsebessége [1/s]
P: gyorsító teljesítmény [W]

A fenti egyenletből ismert adat: a mérőpad tehetetlenségi nyomatéka (thetapad)

Amit mérni lehet: a görgő szögelfordulása az idő függvényében, azaz a  felvétele. 
Ebből már számítható a pad görgőjének mozgásállapota, azaz felvehető az idő függvényében a szögsebesség (omega=f(t)), és a szögsebesség változása (béta=f(t)). A számítás módját lásd fentebb. Így a szögsebesség és szöggyorsulás szorzata a szögsebesség változásának függvényében meghatározható (omega*béta=f(omega)). Ezek alapján a gyorsító teljesítmény egyenletéből már csak a rendszer össztehetetlenségi nyomatéka az, ami nem ismert. Ebből a mérőpad thetája ismert, a hajtáslánc és a motor tehetetlenségi nyomatéka nem. Amennyiben a pad tehetetlenségi nyomatéka kellően nagy értékű a vizsgált jármű thetájához viszonyítva, akkor a számítás végeredményét a jármű ismeretlen értékű thetája kevésbé befolyásolja. A szakirodalom szerint [1] ha a pad tehetetlenségi nyomatéka nagyobb vagy egyenlő a gépjármű összegzett tehetetlenségi nyomatékának (erőforrás + hajtáslánc) tízszeresénél, akkor a diagnosztikai célú teljesítmény ellenőrzéséhez a minimálisan elvárt 5%-os pontosság teljesíthető:

A valóságban a jól kalibrált mérőpad pontatlansága 3% alatt marad. Konkrét példával élve: a Maha gyártmányú LPS 3000 R142, két elektromos örvényáramú fékgéppel rendelkező, összkerékhajtású járművek mérésére (is) alkalmas görgős pad mérési pontossága 2% a mért értékre vonatkoztatva.

A gyorsítás során a motor effektív teljesítménye dinamikus egyensúlyt tart fenn:

1. a hajtáslánc, kerék és próbapad fordulatszám-független veszteségeinek legyőzésére fordított részhányaddal
2. a hajtáslánc, kerék (gumiabroncs) teljesítmény-függő veszteségei legyőzésére fordított részhányaddal
3. a hajtáslánc, kerék (gumiabroncs) és a próbapad fordulatszám (sebesség) függő veszteségei legyőzésére fordított részhányaddal
4. a forgó tömegeket gyorsító részhányaddal

Az 1-3 pont a veszteségteljesítmény (Pveszteség), így képletbe helyezve a fentieket:

 

Szabadkifutás

Teljes terheléses gyorsítás során a leszabályozási fordulatszám elérése előtt az operátor kinyomja a kuplungot. A tengelykapcsoló oldása után a kerekek közel megállásáig mérik a hajtáslánc és görgők szöglassulását. Ebben a szakaszban a motor a tengelykapcsoló segítségével le van választva a hajtáslánc-pad forgó rendszerről:

A szabadkifutás során fellépő fékezőnyomaték:

ahol:
M: a rendszert lassító nyomaték [Nm]
thetarendszer= thetahajtáslánc + thetapad [kgm^2], a görgős pad tengelyére redukálva
béta: kerék (negatív) szöggyorsulása (lassulás) [1/s^2]

A lassítás teljesítményigénye:

ahol:
thetarendszer= thetahajtáslánc + thetapad [kgm^2] a teljes rendszer tehetetlenségi nyomatéka a görgős pad tengelyére redukálva
béta: rendszer (negatív) szöggyorsulása [1/s^2]
omega: a rendszer szögsebessége [1/s]
P: lassító teljesítmény [W]

A gyorsításos szakaszhoz hasonlóan, szabadkifutásban is felvételre kerülnek a , omega=f(t), béta=f(t), omega*béta=f(omega) összefüggések. A mérőpad tehetetlenségi nyomatéka (thetapad) ismert, de továbbra sem ismert a jármű hajtásláncának thetája. Azonban a szabadkifutásra is érvényes az a megállapítás, miszerint ha a pad tehetetlenségi nyomatéka nagyobb vagy egyenlő a gépjármű összegzett tehetetlenségi nyomatékának (jelen esetben csak a hajtáslánc) tízszeresénél, akkor a diagnosztikai célú teljesítmény ellenőrzéshez a minimálisan elvárt 5%-os pontosság teljesíthető.

A szabadkifutás során a fékezőteljesítmény a:

1. a hajtáslánc, kerék és próbapad fordulatszám-független veszteségeinek
2. a hajtáslánc, kerék (gumiabroncs) és a próbapad átvitt teljesítmény-függő veszteségeinek
3. a hajtáslánc, kerék (gumiabroncs) és a próbapad fordulatszám- (sebesség) függő veszteségeinek

összegével egyenlő.

Képletbe helyezve a fentieket:

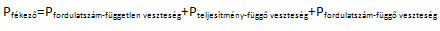 A kérdés az, hogy a gyorsítási folyamatban fellépő veszteségteljesítmény és a szabadkifutás során mérhető fékezőteljesítmény azonos értékű-e? Ha nem, akkor mi a kettő között a különbség? Tegyünk egy kis kitérőt, vizsgáljuk meg a veszteségeket!

Veszteségek

A motor effektív teljesítménye mire eljut a kerék talppontjáig, számos veszteséget szenved el. A veszteségek lehetnek:

1. fordulatszám-független veszteségek
2. az átvitt nyomaték (vonóerő) függvényében kialakuló veszteségek
3. a fordulatszám függvényében kialakuló veszteségek

Fordulatszám-független veszteségek

A fordulatszám-független veszteségek a nyomatékváltó, hajtáslánc, próbapad konstansnak vehető (pl. szimmeringek, tömítések által okozott) veszteségei. A másik két összetevőhöz képest hatásuk nem jelentős.

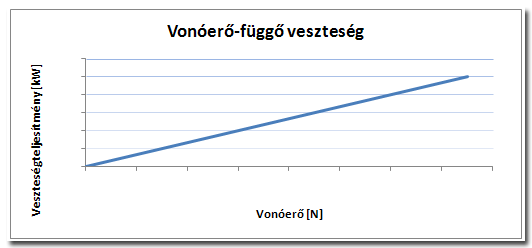
A vonóerő függvényében kialakuló veszteségek

A vonóerő függvényében kialakuló veszteségek a vonóerő nagyságával közel lineárisan változnak. Váltón, differenciálművön  belül  az egymásnak feszülő fogaskerekek fogai között súrlódás lép fel (melyet ugyan a kenőanyag jelentős mértékben csökkent, hatása azonban mérhető), féltengelyek homokinetikus csuklóinál az érintkező, egymáshoz nyomódó felületek mechanikai veszteséget okoznak. Mérés során az egyik legjelentősebb vonóerő-függő veszteség a gumiabroncs - görgő szlip veszteség.

 

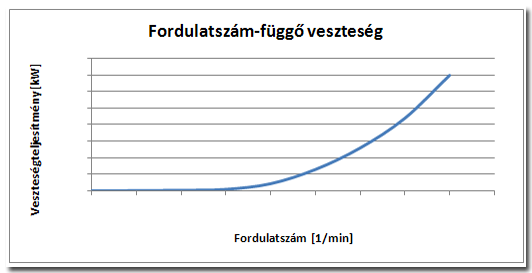
Fordulatszám-függő veszteségek

A fordulatszám-függő veszteségek az olajkavarásból, ventilációból és döntő mértékben a gumiabroncsnak a görgőágyban elszenvedett gyúrásából adódnak (görgős fékpadon történő mérésnél a veszteségteljesítmény nagy hányadát ez teszi ki!). A fordulatszám-függő veszteség nem lineárisan növekedik a sebességgel, hanem a sebesség növekedésével exponenciálisan változik:

 

Visszatérve az eredeti kérdésre: a gyorsítási folyamatban fellépő veszteségteljesítmény és a szabadkifutás során mérhető fékezőteljesítmény azonos értékű-e? A fentiek alapján látható, hogy az átvitt teljesítménytől, vonóerőtől függő veszteség nem lehet azonos, hiszen a rendszert forgatónyomatékot kifejtő motor gyorsítja a mérés gyorsításos részében, aminek hatására a váltó, differenciálmű fogaskerekei egymásnak feszülnek, a féltengelycsuklók alkatrészei egymáson surlódnak stb. Szabadkifutásban ezek a hatások  - a gyorsítás szakaszában átadott nyomatéktől jelentősen kisebb (fékező)nyomaték miatt - kevésbé dominánsan jelentkeznek. A két mérési szakasz veszteségteljesítménye közti eltérést továbbnöveli a két szakasz eltérő összrendszer-thetája, hiszen a gyorsítás során a rendszer teljes tehetetlenségi nyomatékába az erőforrás thetája is beleszámít, míg szabadkifutásban - mely során a motor le van választva a mérőláncról - nem. Mivel a gyorsítás szakaszában a veszteségteljesítmény nem mérhető, így a szabadkifutás során mért veszteséget korrekciós tényezővel figyelembe lehet venni a motor számított effektív teljesítményének meghatározására. A veszteségekről a későbbiekben még ejtünk néhány szót.

Mérési eredmény

A gyakorlatban bevett szokás szerint a motor számított effektív teljesítményének meghatározásakor a gyorsítás és a szabadkifutás során mért teljesítményértékeket összeadják:

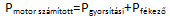ahol:

Pgyorsítási: a gyorsítási szakaszban mért kerékteljesítmény
Pfékező: a szabadkifutás során mért fékezőteljesítmény

Az előző részben már említésre került, illetve a jelen cikk elején is szó volt róla, hogy a teljesítmény származtatott érték:

Így az összetartozó teljesítmény és nyomatékértékek  között minden pontban fennáll a dP/domega=M egyenlőség (a teljesítmény szögsebesség szerinti deriváltja a nyomaték). Mivel a gyorsítási és a szabadkifutási szakaszban ismert a teljesítmény (mért értékek) és ezek összege (számolt érték), ezért nemcsak a főtengelyre vonatkoztatott teljesítményt tudjuk meghatározni, hanem az ehhez a teljesítményhez tartozó (főtengelyre számított) nyomatékot is. Erre a grafikusan ábrázolt mérési eredmény tárgyalásánál még visszatérünk.
Abban az esetben, ha a kiértékeléskor figyelembe veszik a két mérési szakasz közti veszteségkülönbségeket, akkor a motor számított effektív teljesítményét az alábbi módon határozzák meg:

De hangsúlyoznám, hogy általánosságban a főtengelyre visszaszámolt teljesítmény értékének a gyorsítási szakaszban mért kerékteljesítmény és a szabadkifutás során mért fékezőteljesítmény összegét adják meg!

Korrekciós tényező

Mindenki tapasztalhatja, hogy melegben gyengébben teljesít a járműve, csakúgy mint egy magashegyi autós túra alkalmával. A figyelmes vezető azt is észreveheti, hogy párás időben másként gyorsul az autója, mint egy forró nyári napon.  Ezek a hatások érvényesülnek a teljesítménymérés során is. Ha ugyanazt a gépjárművet ugyanazon a teljesítménymérőpadon, de különböző tengerszint feletti magasságokon, külső hőmérsékletek és különböző páratartalom mellett mérnénk, eltérő eredményeket kapnánk.

Azonos nyomáson egységnyi tömegű meleg levegő térfogata nagyobb, mint az alacsonyabb hőmérsékletű levegőé, azaz ugyanakkora  térfogatú mérőedényt (esetünkben hengert) kisebb mennyiségű meleg levegő tölt ki. Ez egyben azt is jelenti, hogy a hengerbe kevesebb oxigén jut be, ami a tüzelőanyag tökéletes elégetése szempontjából elég nagy hátrány. Melegebb beszívott levegő végeredményeként alacsonyabb motorteljesítményt kapunk.
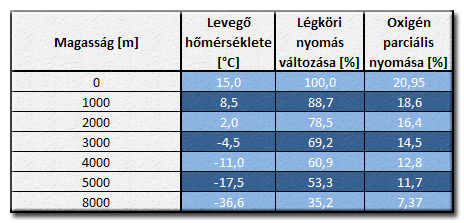
A tengerszint feletti magasság növekedésével a légköri nyomás, a levegő hőmérséklete, a levegő oxigéntartalma, az oxigén parciális nyomása egyre csökken.

A levegő hőmérsékletének, nyomásának változása magasság szerint:

A csökkenő légköri nyomás egyben kisebb relatív nyomáskülönbséget is jelent a henger és a levegőszűrő "előtti" tér nyomása között, összességében csökkentve a hengerbe jutó friss keverék mennyiségét. Ehhez a hatáshoz hozzáadódik a levegő csökkent oxigéntartalmának a következménye is. A motor által leadott teljesítmény szempontjából ezek a hatások negatívumként jelentkeznek. A szakirodalom szerint [4] a tengerszint feletti magasság 100 méterenkénti növekedésével az elszenvedett teljesítményveszteség 1%.
Mindezeket a hatásokat (és ezek kombinációit) a méréskor figyelembe kell venni. Ezért a kapott mérési eredményeket úgynevezett standard atmoszférikus állapotra kell vonatkoztatni korrekciós tényező segítségével. A gépjárműiparban alkalmazott korrekciós eljárások nem egységesek, többféle korrekciós tényező, számolási módszer terjedt el, mint pl. DIN 70020, EWG 80/1269, ISO 1585, SAE J1349, JIS D1001. Ami közös mindegyik eljárásban: figyelembe veszik a mérés helyszínén mért levegőhőmérsékletet és légnyomást (száraz levegőre vonatkoztatva). Amiben viszont különböznek: természetesen a képlet alakjában, valamint eltérőek lehetnek a képletben alkalmazott standard hőmérséklet és légnyomásértékek. Egy példa a korrekciós tényezőre: a The Society of Automotive Engineers (SAE) által 2004 augusztusában frissített SAE J1349 korrekciós formula az alábbi:

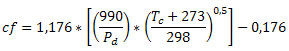ahol:
cf: korrekciós tényező
Pd: légköri nyomás száraz levegőre vonatkoztatva [mb]
Tc: külső hőmérséklet [°C]

A korrekciós tényező alkalmazása: alkalmazhatják keréken mért teljesítményre és főtengelyre vonatkoztatott teljesítményre. Főtengelyre számított teljesítmény esetén a gyorsítási szakaszban mért kerékteljesítmény és szabadkifutás során realizált veszteségteljesítmény összegét megszorozzák a korrekciós tényező értékével, a szorzat értéke az úgynevezett korrigált motorteljesítmény. Azaz:

ahol:
cf: korrekciós tényező

Egyes teljesítménymérő padokon lehetőség van nem szabványos korrekciós tényezők használatára is.

Korrekciós tényező alkalmazásának előnye a gyakorlatban

Miért jó, ha korrekciós tényezőt alkalmazunk? Tegyük fel, hogy autónkat teljesítménynövelő tuning előtt kimondottan hűvös, páradús időben mérettük le. A főtengelyre számított teljesítmény 105 kW-ra adódott. A motor kisebb mértékű átalakítása után (pl. hengerfejjáratok portolása, polírozása, nagyobb átmérőjű szívószelepek alkalmazása) szeretnénk papíron látni, hogy mekkora pozitív változást sikerült elérni. Az ismételt mérésre ugyanazon a padon, a motortuningot nem számítva változatlan járművel, de forró nyári kánikulában kerül sor, a mért teljesítmény főtengelyre számítva 107 kW. Korrekciós tényező használata nélkül ebben az esetben csak reménykedni tudunk abban, hogy az eltérő mérési körülmények okozták a csalódást okozó, igen kismértékű teljesítménynövekményt. Ha mindkét méréskor éltünk volna a korrekció lehetőségével, akkor az első mérés során 101 kW csúcsteljesítményt, a második mérés során 109 kW-ot realizálhattunk volna (a közölt értékek nem valós mérésen alapulnak, csak szemléltető jellegűek), amiből már egyértelműen látható, hogy érdemes volt elvégezni a motoron az átalakításokat. Röviden: korrekciós tényező segítségével minimalizálható a légköri körülmények (légnyomás, páratartalom, hőmérséklet) befolyásoló hatása.

A mért értékek grafikus megjelenítése

A mért értékek megjelenítésére a legelterjedtebb - és a legkönnyebben átlátható - megoldás a derékszögű koordináta rendszerben történő ábrázolás. A koordináta rendszer x tengelyén a fordulatszám van feltüntetve, míg az y tengely kettős skálázásán a nyomaték  és a teljesítmény. A lentebb közölt  diagram bal oldali y tengelyén a nyomaték, a jobb oldalin a teljesítmény van került ábrázolásra.
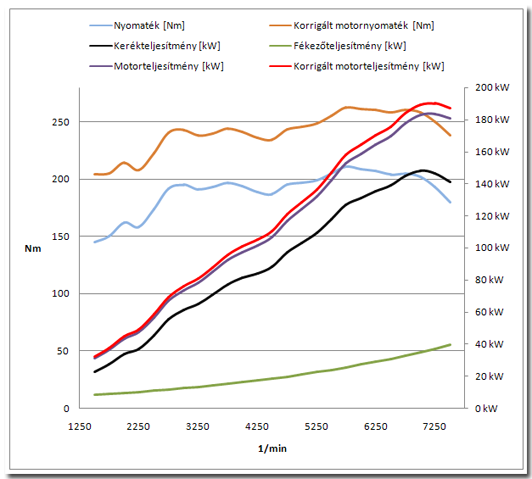
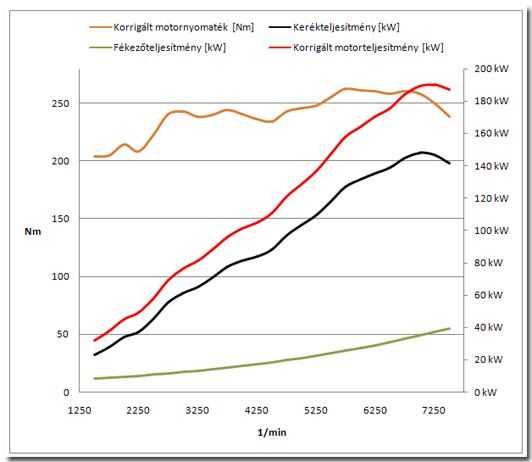
A grafikusan megjelenített mérési eredmények megértéséhez vizsgáljunk meg egy olyan dyno diagramot, melyen az alábbi értékek vannak feltüntetve: a keréken mért nyomaték, a keréken mért teljesítmény, a fékezőteljesítmény, a főtengelyre vonatkoztatott motorteljesítmény, a korrigált motorteljesítmény, a korrigált motornyomaték.  A valóságban ilyen párosításban nem szokás megadni a nyomatékértékeket; ha a szerepel a korrigált teljesítményérték a diagramon, akkor a korrigált motornyomatékot szokás ábrázolni, a keréken mért nyomatékot nem.

A grafikonon a világoskék vonal mutatja a keréken mért nyomaték értékét a fordulatszám változásának függvényében. A fekete vonal a keréken mért teljesítményt reprezentálja. Matematikában jártas szemlélőnek feltűnhet a két vonal közti közvetlen kapcsolat, a teljesítmény görbéjének szögsebesség (fordulatszám) szerinti deriváltja a nyomatéki görbe (hiszen P= M*omega=M*2*n*pi/60; a görbe minden pontjában fennáll a dP/domega=M kapcsolat). A lila vonal a főtengelyre számított motorteljesítmény, amelyről már tudjuk, hogy a keréken mért teljesítmény és a szabadkifutásban mért fékezőteljesítmény (zöld vonal) összege.
A fékezőteljesítmény ábrázolása esetenként a koordinátarendszer y tengelyének negatív tartományában kerül feltüntetésre, ezzel is szemléltetve, hogy veszteségről van szó. A mellékelt diagramon pozitív előjellel került ábrázolásra. Nézzük meg alaposabban a szabadkifutás során mért eredmény görbéjét: jól megfigyelhető a magasabb fordulatszám-tartományban mért nagyobb veszteség, a görbe exponenciális jellegű, a fordulatszám növekedésével nem lineárisan növekedik az értéke. Ha visszaemlékszünk: a fékezőteljesítmény konstans-, fordulatszámfüggő- és átvitt teljesítménytől függő komponensek összege. A fordulatszámfüggő komponens lineáris, míg a teljesítménytől függő exponenciális jellegű.
A főtengelyre visszaszámolt teljesítmény (lila görbe) minden pontjában fennáll a Pmotor számított=Pgyorsítási+Pfékező összefüggés, azaz a lila görbe adott fordulatszámhoz tartozó értéke a fekete és a zöld görbe ugyanahoz a fordulatszámhoz tartozó értékeinek az összege. Mivel a veszteségek a fordulatszámmal nem lineárisan növekednek, ezért a főtengelyre számított érték görbéjének alakja valamelyest eltér a magasabb fordulatszám-tartományban a fekete görbe alakjától. A mellékelt diagramon jól látható az ebből származó differencia: a teljesítménymaximum után a keréken mért teljesítmény meredekebben esik, mint a főtengelyre vonatkoztatott teljesítmény görbéje (lila).
A piros görbe a korrigált teljesítmény görbéje, mely a  lila görbének korrekciós tényezővel vett szorzata. Fentebb már szó esett a teljesítmény és a nyomaték közvetlen kapcsolatáról. Ez a korrigált motorteljesítmény esetén is igaz, ezért az adott fordulatszámhoz tartozó korrigált teljesítmény ismeretében számítással meghatározható a vizsgált fordulathoz tartozó korrigált motornyomaték (narancssárga görbe).

Komoly szoftverrel (és kiegészítő mérőberendezésekkel) felszerelt pad mérési diagramjára számos adat kerülhet fel a teljesítményen és nyomatékon kívül. Néhány ilyen adat a teljesség igénye nélkül: gázpedálállás, AFR, turbonyomás / szívócső-depresszió, kipufogógáz-hőmérséklet, előgyújtás értéke. Az operátor dönti el, hogy ezek közül melyek szerepeljenek az eredménydiagramon. Azonban az alábbiak feltüntetése a leggyakoribb: keréken mért teljesítmény, fékezőteljesítmény, korrigált motorteljesítmény, korrigált motornyomaték. Ezekkel az eredményekkel a fenti diagram:

 

Természetesen olyan is előfordulhat, amikor csak a keréken mért értékek kerülnek ábrázolásra. A kívánt mérési feladattól függ, hogy mit tart az operátor fontosnak rögzíteni.

Az elsőre kissé bonyolultnak tűnő méréssel kapcsolatos egyik leggyakoribb kérdés: miért van szükség többféle teljesítményt mérni, ezeket összeadni, korrigálni stb., mikor a valóságban úgy is csak a keréken kifejtett (mért) vonóerő, nyomaték, teljesítmény a fontos? A felvetés teljesen jogos! Válasszuk szét egymástól a mérés pontosságát, megismételhetőségét, a mérési eredmények összehasonlíthatóságát.
Kezdjük a mért értékek pontosságával! A cikk elején említett példában már szóba került: a görgős padon mért kerékteljesítmény is csak közelíti a valóságost, mivel a gumiabroncs a görgőágyban nagyobb deformációt  szenved el (több "hasznos" teljesítményt nyel el), mint közúton.  A főtengelyre visszaszámolt teljesítménnyel szemben a kerékteljesítmény "nyersebb", kevésbé szofisztikált. Emlékezzünk vissza: a görgős padon történő teljesítménymeghatározásnál a főtengelyre számolt érték a kerékteljesítmény és a szabadkifutás során (terheletlen hajtáslánc) mért teljesítmények összege. Ahogy láthattuk, a gyorsításos és szabadkifutásos veszteségteljesítmény nem azonos. Már maga a keréken mért teljesítmény is egy bizonyos nagyságú hibával terhelt, ha a közúton leadott kerékteljesítményt vesszük alapnak. Főtengelyre vonatkoztatásnál ehhez még hozzáadódik egy olyan veszteségteljesítmény, melynek értéke szintén csak közelíti a valóságost (mert az alkatrészeket nem szorítja egymásnak a motor nyomatéka ebben a mérési fázisban). Így főtengelyre vonatkoztatott értéknél ezek a pontatlanságok összeadódnak.
Az egy- és kétgörgős padok összehasonlításánál látni fogjuk, hogy  az egygörgős kerékgyúrása kisebb, jobban közelíti a közúton fellépőt. A pad típusától és a görgőágy kialakításától függetlenül eltérő kerékteljesítményt mérhetünk egyazon járművön és mérőpadon már akkor is, ha két, egymást követő mérés során nem azonos a gumiabroncs típusa, mérete ("ballonos" és "peres" gumi oldalfalmerevségének különbsége) vagy a gumiabroncsnyomások nagyobb mértékben eltérnek. Ezen zavaró tényező ellen egyszerűen védekezhetünk, ha a mérések során ugyanazt az abroncsot, ugyanakkora nyomáson használjuk. Így a mérés korrekt megismételhetőségét biztosítani tudjuk azonos jármű esetén, kiváltképp, ha a vizsgálatok azonos légköri körülmények között történnek, vagy élünk a korrekció lehetőségével. Azonban, ha két különböző jármű kerékteljesítményét szeretnénk összemérni, akkor ez a módszer nem igazán használható. Tudjuk, hogy gyorsítás során az egymásnak feszülő alkatrészeken súrlódás lép fel (lényegében hőenergiává alakul át a mozgási energia). Ezért ha két, főtengelyen (ténylegesen) azonos teljesítményű, minden paraméterükben azonos kerekekkel szerelt, de eltérő felépítésű hajtáslánccal rendelkező járműveket vizsgálunk, akkor különböző kerékteljesítményértékeket mérhetünk. Elég, ha a váltó felépítése, áttétele különbözik. Ez a tény megnehezíti a mérési eredmények összehasonlíthatóságát.

Hajtásláncveszteség mérésének szükségessége

Itt kapcsolódik be a hajtásláncveszteség mérésének fontossága: a veszteségek rögzítésével majd a kapott eredményeknek főtengelyre történő átszámításával (és korrekciójával) a hajtásláncveszteségek egy része és a görgőágyban fellépő veszteségek kompenzálhatóak. Az alábbi gyakorlati példában az egyszerűség kedvéért ugyanazt a gépjárművet eltérő méretű abroncsokkal vizsgáljuk: gépjárművünk teljesítményét egymás után kétszer leméretjük, az első mérés alkalmával 195/50 R15-ös, 3 barra fújt gumiabroncsokkal állunk rá a padra. Első nekifutásra a keréken mért teljesítményre 94 kW adódik, a veszteségteljesítményre pedig 16 kW (csak szemléltető adat, nem valós eredményen alapuló érték). Második menet előtt autónkon kereket cserélünk, 215/40 R16-os, 2 barra  pumpált gumik kerülnek rá. Ezzel a setuppal a keréken mért teljesítmény 89 kW-ra adódik. Hová lett 5 kW-nyi (hasznos) teljesítmény? A válasz: bár a két gumiméret egymásnak váltómérete, azonban a kerekek tömege, tehetetlenségi nyomatéka, a gumik anyaga, az abroncsnyomás, a gumik oldalfalának merevsége eltér, így különböző lesz a mért fékezőteljesítmény (hajtásláncveszteség) is, ami a második mérés során 21 kW-ot tesz ki. Ha összeadjuk a mért értékeket, azt tapasztaljuk, hogy: 94 + 16 = 89 + 21= 110 kW főtengelyen, azaz a motor ugyanannyit teljesít mindkét esetben, de ennek csak kisebb hányada jutott el a kerék talppontjáig a második mérés során.

Az olvasóban felmerülhet a kérdés, hogyha ismert egy adott járműnek a fékezőteljesítménye (a hajtáslánc szabadkifutásban mért veszteségteljesítménye a főtengelyre számított teljesítmény százalékában megadva) akkor ezt miért nem lehet felhasználni egy másik, hasonló hajtáslánccal rendelkező jármű mérésénél?! Elég lenne csak a keréken mért teljesítményt mérni, és a százalékosan ismert fékezőteljesítményt felhasználva számolással meg is kapnánk a főtengelyen levehető teljesítmény értékét. Így nem lenne szükség a szabadkifutás elvégzésére.
Ami problémás ezzel az eljárással: már láthattuk a veszteségteljesítmény "összetételét": van konstans tagja, emellett létezik lineárisan növekvő része és van exponenciálisan változó összetevője. A százalékos számolás alkalmazása a veszteségtagokra pontatlan eredményt ad. A százalékos értékről ezért azt is tudni kellene, hogy mekkora fordulaton értendő. Minimum több fordulatszámon kellene ismernünk a veszteség %-os értékét ahhoz, hogy a le nem mért szabadkifutásos fékezőteljesítmény görbéjének alakját közelítsük. Ha csak azt mondjuk, hogy a százalékban kifejezett veszteség 20% és ezzel számolunk a keréken mért teljesítmény görbéjének minden pontjában, akkor csak egyszerű  közelítést végeztünk, ami - ahogy már láthattuk - nem igaz a veszteség görbéjére. Ezért ez a megoldás csak durva közelítést ad, pontos mérési eredmény felvételére alkalmatlan. Gyakorlatban azért szokták mégis emlegetni, mert egy adott járműtípusra ismert ennek a "tól-ig" értéke, így a mérés végrehajtásakor a mérés és a hajtáslánc "jóságát" meg tudjuk ítélni. Pl. ha tudjuk, hogy egy járműre 21-25%-os hajtásláncveszteség jellemző, ám mérésünkkor 34%-os veszteséget mértünk, akkor erősen gyanakodhatunk, hogy valami nem stimmelt a mérés során.

Összefoglalva a fentieket: a kerékteljesítmény kevésbé mesterkélt eredményt ad, mint a főtengelyre számított effektív motorteljesítmény. Két jármű "közúti" teljesítményének összehasonlítására alkalmasabb, mint a motorteljesítmény, ha a két jármű azonos (de minimum megegyező felépítésű görgőággyal szerelt) padon lett mérve. Ugyanannak a járműnek eltérő időpontokban mért kerékteljesítmény értékei akkor hasonlíthatóak össze egymással megfelelő pontossággal, ha a mérések között a gépkocsi hajtáslánca, kereke, abroncsnyomása nem lett módosítva. A főtengelyre számított teljesítmény pontosabb összevetést tesz lehetővé két jármű motorteljesítménye között, mivel kompenzálja az eltérő kerekek, hajtáslánc miatt fellépő különböző mértékű veszteségteljesítményeket. Ugyanebből kifolyólag egyazon jármű két időpontban felvett motorteljesítménye is pontosabban összehasonlítható, a mérési eredmény könnyebben reprodukálható. Természetesen mindegyik említett mérési eredmény azonos korrekciós tényezővel vett eredmény.

Méréssorozat a gyakorlatban

Az egyik alapszabály, ami a mérési eredmények összehasonlíthatóságát illeti: teljesítménynövelő tuning előtt és után mindig ugyanazon a padon méressük le járművünket, ha lehetséges! Az egyes padok kalibrációja, esetleges mérési pontatlansága kisebb mértékben eltérhet egymástól. Főként igaz ez a fékgéppel rendelkező padokra, ahol a fékgép (esetleges) apróbb működési rendellenessége, az erőmérő cella pontatlansága a mérési eredményre kihatással lehet (nem nagy, alig 1-2 százaléknyi eltérésről van csak szó, ám nagy teljesítményű jármű esetén ez számszerűleg már több kW-nyi differenciát eredményezhet). Ugyanazon a padon ezek a pontatlanságok későbbi mérés során is jelentkeznek. Így bár két mérési hibával terhelt eredményt kapunk, de az eredmények egymással összevethetőek lesznek. Ebből a szempontból előnyösebbek az instacioner padok, mivel azokon a fékgép, erőmérő cella alkalmazásából eredő rejtett hibák nem jelentkeznek. Ha azonos görgővel (méret, anyag, kialakítás) rendelkezik két instacioner pad, akkor a görgők tehetetlenségi nyomatéka (elméletileg és gyakorlatilag is) ugyanakkora, így a járműnek gyorsítás során - bár különböző padokon kerül mérésre - azonos nagyságú erőket kell leküzdenie.

A görgőágyban fellépő erők

Bár ez az írás elsősorban a kétgörgős, instacioner padon történő teljesítménymérésről szól, azért a teljesség igénye miatt vizsgáljuk meg röviden a különbségeket az egygörgős (single roll) és kétgörgős (tandem roll) görgőággyal szerelt padok között.

Egygörgős kivitel (emelhető mérőpad):

 

Kétgörgős kivitel:

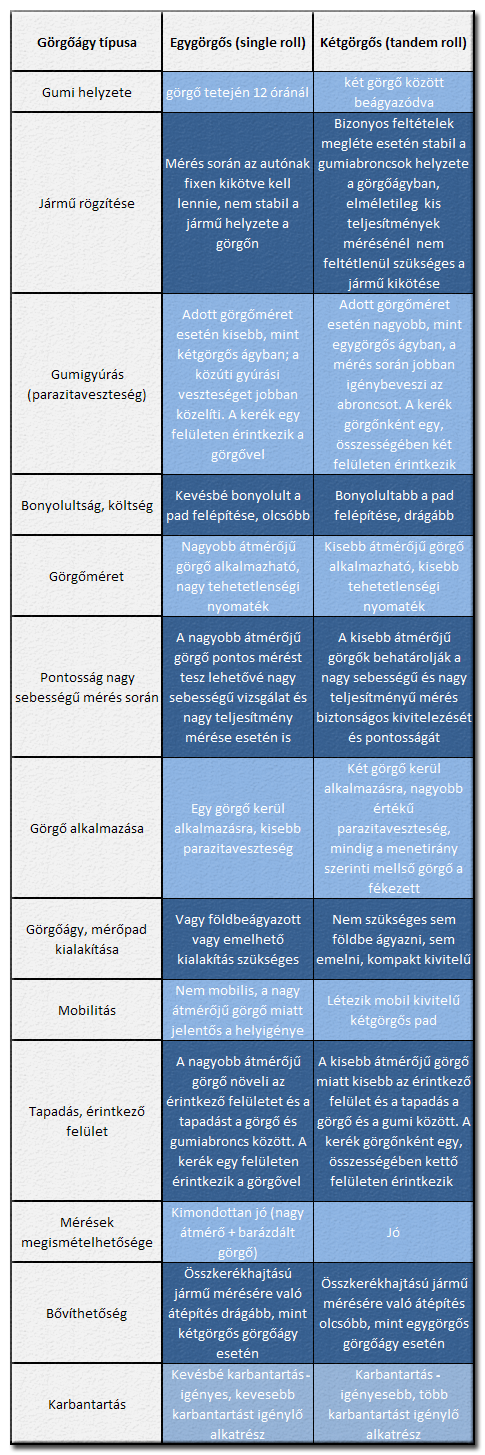
A görgőágyak közti főbb különbségek

A továbbiakban csak kétgörgős görgőágyban fellépő erőkről lesz szó. Nyugalmi helyzetben az alábbi statikus egyenlőség áll fenn egy szokásos kialakítású kétgörgős görgőágyban (azonos méretű görgők, szinteltolás nincs, a kerék szimmetrikusan ül a görgők között):

ahol:
G: függőleges kerékterhelés [N]
N1: támasztóerő [N]
N2: támasztóerő [N]

A függőleges kerékterhelés, a görgők átmérőjének, egymástól való távolságának és a gumiabroncs méretének ismeretében a támasztóerők számolhatóak, a kerékterhelés és az N1 támasztóerő által bezárt szög (elhelyezkedési szög) meghatározható.  A görgő maximális tapadási tényezője ismert. A járműkerék helyzete stabil a görgőágyban, ha teljesül a:

reláció, ahol:
: görgő tapadási tényezője
tg alfa: elhelyezkedési szög tangense

A stabilitás ellenére a jármű spaniferrel történő rögzítése előírás. Az autó kikötése oly módon történik, hogy a vizsgált jármű sem előre-hátra, sem oldalirányba ne tudjon elmozdulni. Nagy teljesítményű járművek mérésénél előfordulhat, hogy kiegészítő súlyokkal növelik meg a jármű tömegét a nagyobb tapadóerő érdekében.

Vizsgáljuk meg a fékpad görgőágyán maximálisan átvihető nyomatékot és vonóerőt!  Mérés közben fellépő erők a görgőágyban:

ahol:
G: függőleges kerékterhelés [N]
N1: támasztóerő [N]
N2: támasztóerő [N]
Fv: vonóerő [N]

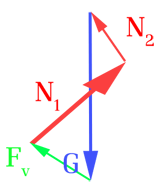
Szemléletesebb, ha élünk a szabad vektorok által biztosított lehetőséggel és az erővektorokat eltoljuk egymás végpontjaiba. Stabil kerékhelyzet esetén a vektorok zárt rendszert alkotnak:

Ahogy már láttuk: a rendszer stabil marad mindaddig, míg fennáll a  reláció. 3 eset lehetséges:

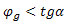1.  esetén a rendszer mindvégig stabil marad. Az N2 támasztóerő nem csökken le túlságosan. A gépkocsi nem lép ki a görgőágyból, további vonóerőnövelésnél a gumiabroncs megcsúszik a görgőn.
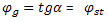2. , ahol 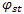a stabilitási határhoz tartozó tapadási tényező ? Az elhelyezkedési szög tangense azonos értékű a görgő tapadási tényezőjével, a rendszer stabilitásának határán van. Ekkor N2=0.
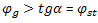3. esetén a rendszer instabil, a kerék kilép a görgőágyból  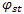felett.

Kerékterhelés kihasználási tényező

A fentebb említett elhelyezkedési szög meghatározása, stabilitás ellenőrzése mellett számos egyéb paramétert lehet számolni. Mivel ezen paraméterek ismertetése bőven meghaladná ennek az írásnak a kereteit, ezért csak az egyik legfontosabb tényező ismertetésére kerül sor néhány szóban. Ez pedig az úgynevezett kerékterhelés kihasználási tényező, ami százalékos formában megadja, hogy a kifejthető vonóerő hány százaléka a kerékterhelésnek:

ahol:
qF:kerékterhelés kihasználási tényező [%]
Fmax: vonóerő maximuma [N]
Gk: kerékterhelés [N]
: görgő tapadási tényezője
alfa: elhelyezkedési szög [°]

A kerékterhelési kihasználási tényező a görgőágy és a görgőágyban elhelyezkedő kerék együttes geometriájának a függvénye.

A mérés kivitelezése előtt a jármű előzetesen ismert legnagyobb nyomatéka és hajtásláncának áttétele alapján meg tudjuk határozni a stacioner pad által az egyes fokozatokban lefékezendő teljesítményt. A fékgép jellegmezője segítségével így kideríthető, hogy a keréken kifejtett teljesítmény lefékezhetó-e az egyes fokozatokban a stacioner mérési eljárás során. A jellegmezőről, illetve a fékgép alkalmazhatóságáról az előző részben esett szó.

A gépjármű igénybevétele

Végül essen szó a jármű mérés közbeni igénybevételéről. Jobb helyeken a mérés előtt a járművet átvizsgálják: nézik a gumik állapotát, típusát, sebességindexét. Olajfolyás esetén a gépjármű nem állhat fel a padra. Egy átlagos mérés - padraállással, a jármű rögzítésével, a motor bemelegítésével (ha szükséges), méréssel együtt - általában nem tart tovább fél óránál, mely idő során az erőforrás ténylegesen, nagy igénybevétellel csak néhány percig van terhelve. Összességében néhány perces autópályahasználathoz hasonlítható a gépjármű mérés közbeni igénybevétele. Értő kezelőszemélyzet felügyelete mellett az autó nem tehető tönkre a padon.

---

Konklúzió

Már Magyarországon is egyre több gépjárművekkel foglalkozó műhely alkalmaz görgős fékpadot. Egy jól  felszerelt fékpad megfelelően képzett kezelőszemélyzettel igen komoly "fegyver" lehet a padot nem használó versenytársakkal szemben. Ahogy láthattuk, a (stacioner) padok alkalmazási köre nem kimondottan csak a teljesítménymérésre korlátozódik, a járműdiagnosztikában, egyes hibák feltárásában is nagy segítségre van.
Bár nem érintettük a teljesítménymérés és görgős fékpadok alkalmazásának teljes témakörét, ennek ellenére bízom benne, hogy sikerült ezzel a kétrészes írással minden olvasónak átfogóbb képet kapnia a padok felhasználási területéről, a teljesítménymérés elvi alapjairól és gyakorlati kivitelezéséről.